As questões de Funções no Enem é um dos temas mais abordados na prova de Matemática do exame. Por isso, se você deseja obter uma boa nota, estudar esse assunto é essencial.
Conceitualmente, a Função é a relação entre dois conjuntos, denominados domínio e e contradomínio. Para cada domínio há um elemento correspondente no contradomínio.
Esse conceito de função é cobrado no Enem em questões que envolvem desafios do cotidiano, exigindo, na maioria das vezes, a interpretação de texto do aluno. Além disso, toda função pode ser expressa na forma de gráficos, sendo outro aspecto exigido do aluno nos exercícios.
Existem no total 15 tipos funções matemáticas, porém as mais cobradas nas questões são: função afim (primeiro grau), função quadrática (segundo grau), função logarítmica e função exponencial.
Separamos uma lista com 14 questões de funções das últimas provas do Enem para você testar seus conhecimentos sobre o assunto. Para ver o gabarito e ver a resolução completa da questão, basta clicar em “Ver reposta“.
Resolva questões de Funções no Enem

- Questões de Funções Inorgânicas no Enem
- Questões de Probabilidade no Enem
- Matemática Básica no Enem: O que estudar
Questão 01
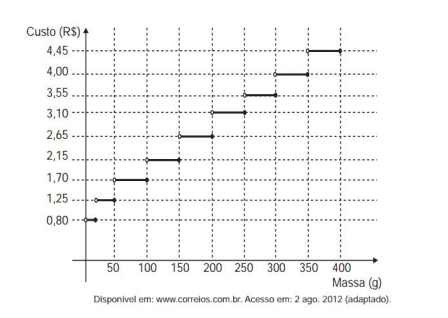
(Enem) Deseja-se postar cartas não comerciais, sendo duas de 100 g, três de 200 g e uma de 350 g. O gráfico mostra o custo para enviar uma carta não comercial pelos Correios:
O valor total gasto, em reais, para postar essas cartas é de
a. 8,35.
b. 12,50.
c. 14,40.
d. 15,35.
e. 18,05.
Veja o vídeo de resolução:
Questão 02
(Enem 2021) Uma pessoa pretende viajar por uma companhia aérea que despacha gratuitamente uma mala com até 10 kg.
Em duas viagens que realizou essa pessoa utilizou a mesma mala e conseguiu 10 kg com as seguinte combinações de itens:
| Viagem | Camisetas | Calças | Sapatos |
| I | 12 | 4 | 3 |
| II | 18 | 3 | 2 |
Para ter certeza de que sua bagagem terá massa de 10 kg, ela decide levar essa mala com duas calças, um sapato e o máximo de camisetas, admitindo que itens do mesmo tipo têm a mesma massa.
Qual a quantidade máxima de camisetas que essa pessoa poderá levar?
a. 22
b. 24
c. 26
d. 33
e. 39
Veja o vídeo de resolução:
Questão 03
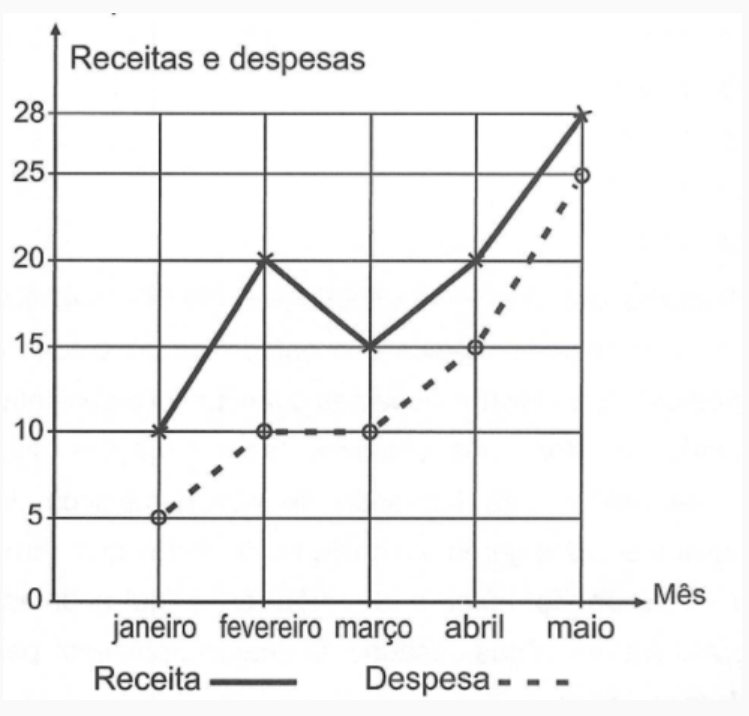
(Enem 2021) A receita R de uma empresa ao final de um mês é o dinheiro captado com a venda de mercadorias ou com a prestação de serviços nesse mês, e a despesa D é todo o dinheiro utiliado para pagamento de salários, contas de água e luz, impostos, entre outros. O lucro mensal obtido ao final do mês é a diferença entre a receita e a despesa registradas no mês. O gráfico apresenta as receitas e despesas, em milhão de real, de uma empresa ao final dos cinco primeiros meses de um dado ano.
A previsão para os próximos meses é que o lucro mensal não seja inferior ao maior lucro obtido até o mês de maio.
Nessas condições, o lucro mensal para os próximos meses deve ser maior ou igual ao do mês de
a. Janeiro.
b. Fevereiro.
c. Março.
d. Abril.
e. Maio.
Veja o vídeo de resolução:
Questão 04
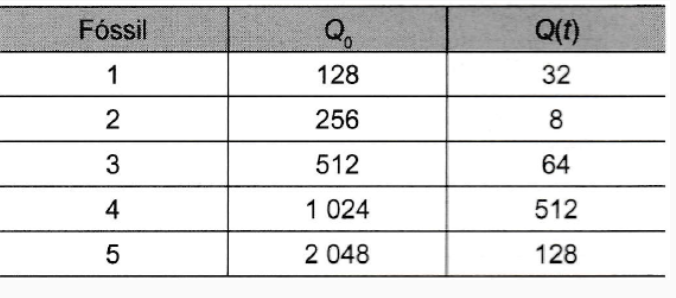
(Enem 2020) Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ela morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5 730 anos, ou seja, num fóssil de um organismo que morrei há 5 730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: Q(t)=Q0.2−t5730Q(t)=Q0.2−t5730 em que tt é o tempo, medido em ano, Q(t) é a quantidade de carbono 14 medida no instante e t Q0 é a quantidade de carbono 14 no ser vivo correspondente.
Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existentes. Na tabela temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.
O fóssil mais antigo encontrado nessa expedição foi:
a. 1
b. 2
c. 3
d. 4
e. 5
Veja o vídeo de resolução:
Questão 05
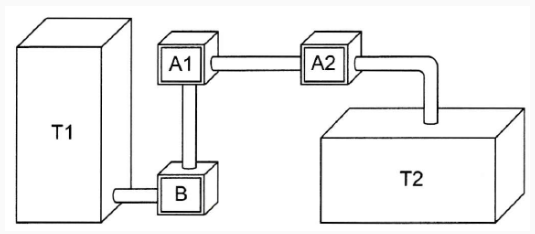
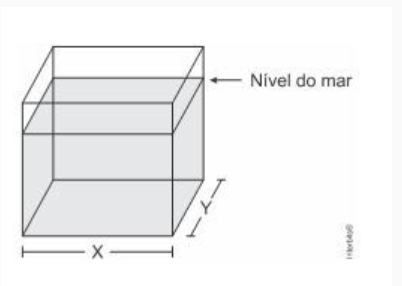
(Enem 2020) Um processo de aeração, que consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, que aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acordo com a figura.
Os tanques T1 e T2 são prismas retos de bases retangulares, sendo que a base de T1 tem comprimento c e largura L, e a base de T2 tem comprimento c2c2 e largura 2L.
Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido que já saiu de T1, denotada por x, e a altura da coluna de líquido que chegou a T2, denotada por y.
Disponível em: www.dec.ufcg.edu.br. Acesso em 21 abr. 2015.
A equação que relaciona as medidas das alturas y e x é adaptada por
a. y = 1,265x
b. y = 1,250x
c. y = 1,150x
d. y = 1,125x
e. y = x
Veja o vídeo de resolução:
Questão 06
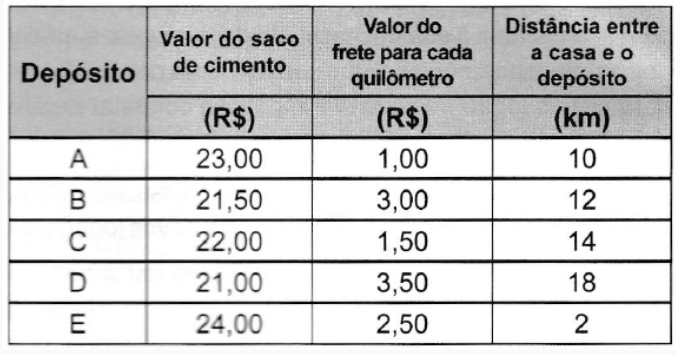
(Enem 2020) Uma pessoa precisa comprar 15 sacos de cimento para uma reforma em sua casa. Faz pesquisa de preço em cinco depósitos que vendem o cimento de sua preferência e cobram frete para entrega do material, conforme a distância do depósito à sua casa. As informações sobre preço do cimento, valor do frete e distância do depósito até a casa dessa pessoa estão apresentadas no quadro.
A pessoa escolherá um desses depósitos para realizar sua compra, considerando os preços do cimento e do frete oferecidos em cada opção.
Se a pessoa decidir pela opção mais econômica, o depósito escolhido para a realização dessa compra será o
a. A
b. B
c. C
d. D
e. E
Veja o vídeo de resolução:
Questão 07
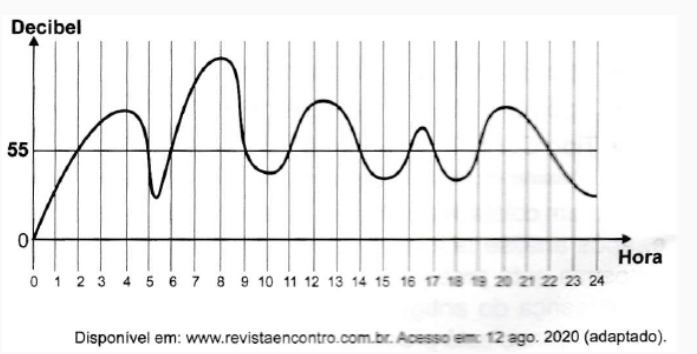
(Enem 2020) A exposição a barulhos excessivos, como os que percebemos em geral em trânsitos intensos, casas noturnas e espetáculos musicais, podem provocar insônia, estresse, infarto, perda de audição, entre outras enfermidades. De acordo com a Organização Mundial da Saúde, todo e qualquer som que ultrapasse os 55 decibéis (unidade de intensidade do som) já pode ser considerado nocivo para a saúde. O gráfico foi elaborado a partir da medição do ruído produzido, durante um dia, em um canteiro de obras.
Nesse dia, durante quantas horas o ruído esteve acima de 55 decibéis?
a. 5
b. 8
c. 10
d. 11
e. 13
Veja o vídeo de resolução:
Questão 08
(Enem 2019) Charles Richter e Beno Gutenberg desenvolveram a escala Richter, que mede a magnitude de um terremoto. Essa escala pode variar de 0 a 10, com possibilidades de valores maiores. O quadro mostra a escala de magnitude local (MsMs) de um terremoto que é utilizada para descrevê-lo.
| Descrição | Magnitude Local(MsMs)(μm⋅Hz)μm⋅Hz) |
|---|---|
| Pequeno | 0⩽Ms⩽3,90⩽Ms⩽3,9 |
| Ligeiro | 4,0⩽Ms⩽4,94,0⩽Ms⩽4,9 |
| Moderado | 5,0⩽Ms⩽5,95,0⩽Ms⩽5,9 |
| Grande | 6,0⩽Ms⩽9,96,0⩽Ms⩽9,9 |
| Extremo | Ms⩾10,0Ms⩾10,0 |
Para se calcular a magnitude local, usa-se a fórmula = 3,30 + log (A.f), em que
representa a amplitude máxima da onda registrada por um sismógrafo em micrômetro(
Utilize 0,3 como aproximação para log 2. De acordo com os dados fornecidos, o terremoto ocorrido pode ser descrito como:
a. Pequeno.
b. Ligeiro.
c. Moderado.
d. Grande.
e. Extremo.
Veja o vídeo de resolução:
Questão 09
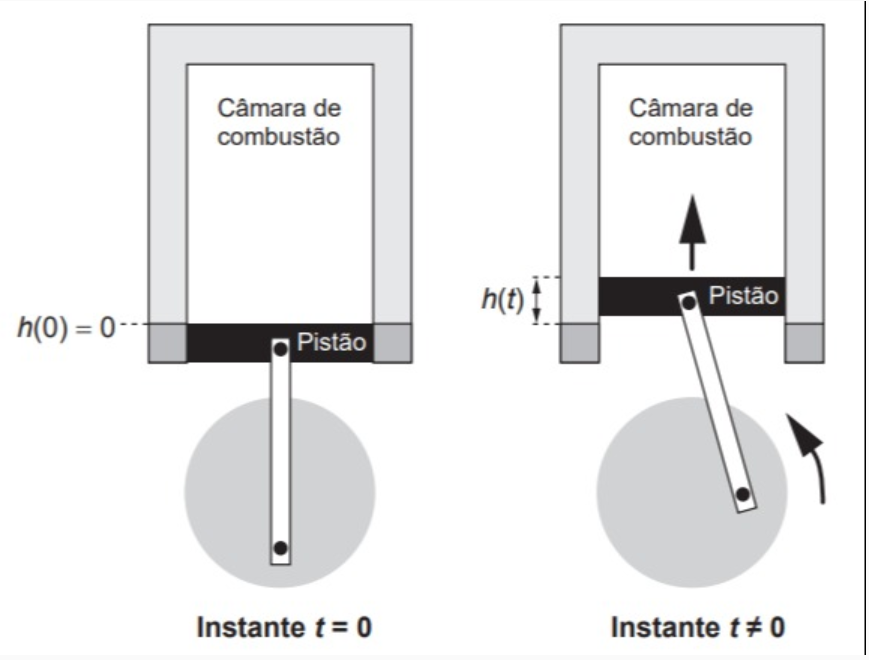
(Enem 2019) Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.
A função h(t)=4+4sin(βt2−π2)h(t)=4+4sin(βt2−π2)definida para t ≥ 0 descreve como varia a altura h, medida em centímetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.
O valor do parâmetro BETA, que é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para que o motor tenha uma boa potência, é necessário e suficiente que, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm. Para os cálculos, utilize 3 como aproximação para ππ.
O menor valor inteiro a ser atribuído ao parâmetro ββ, de forma que o motor a ser construído tenha boa potência, é:
a. 1
b. 2
c. 4
d. 5
e. 8
Veja o vídeo de resolução:
Questão 10
(Enem 2017) Viveiros de lagostas são construídos, por cooperativas locais de pescadores, em formato de prismas reto-retangulares, fixados ao solo e com telas flexíveis de mesma altura, capazes de suportar a corrosão marinha. Para cada viveiro a ser construído, a cooperativa utiliza integralmente 100 metros lineares dessa tela, que é usada apenas nas laterais.
Quais devem ser os valores de X e de Y em metro, para que a área da base do viveiro seja máxima?
a. 1 e 49.
b. 1 e 99.
c. 10 e 10.
d. 25 e 25.
e. 50 e 50.
Veja o vídeo de resolução:
Questão 11
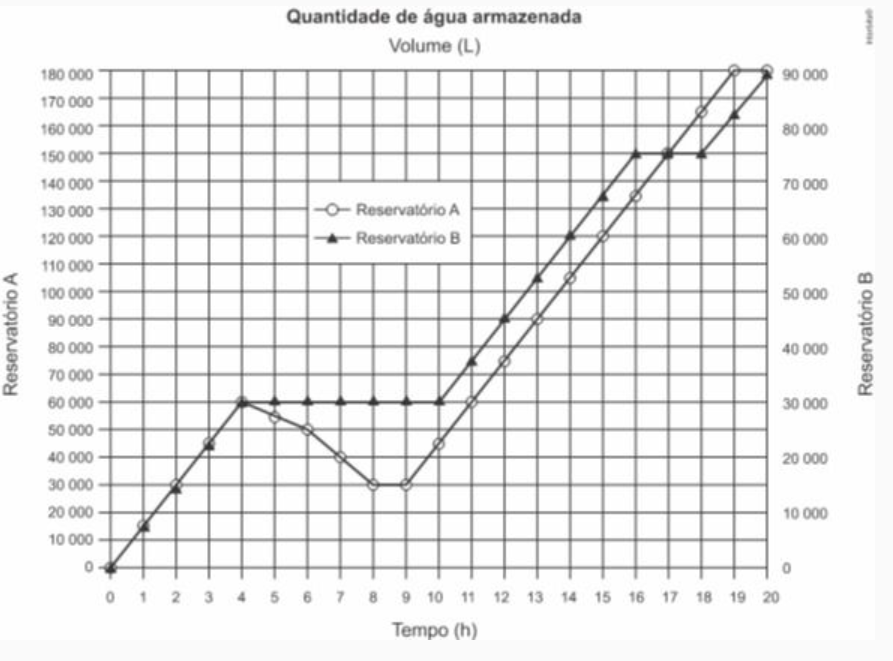
(Enem 2017) Dois reservatórios A e B são alimentados por bombas distintas por um período de 20 horas. A quantidade de água contida em cada reservatório nesse período pode ser visualizada na figura.
O número de horas em que os dois reservatórios contêm a mesma quantidade de água é
a. 1
b. 2
c. 5
d. 5
e. 6
Veja o vídeo de resolução:
Questão 12
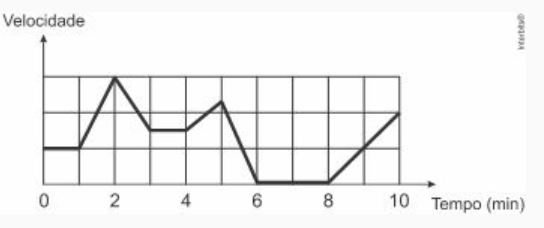
(Enem 2017) Os congestionamentos de trânsito constituem um problema que aflige, todos os dias, milhares de motoristas brasileiros. O gráfico ilustra a situação, representando, ao longo de um intervalo definido de tempo, a variação da velocidade de um veículo durante um congestionamento.
Quantos minutos o veículo permaneceu imóvel ao longo do intervalo de tempo total analisado?
a. 4
b. 3
c. 2
d. 1
e. 0
Veja o vídeo de resolução:
Questão 13
(Enem 2016) Uma liga metálica sai do forno a uma temperatura de 3000 ºC e diminui 1% de sua temperatura a cada 30min.
Use 0,477 como aproximação para log10(3) e 1,041 como aproximação para log10(11).
O tempo decorrido, em hora, até que a liga atinja 30 °C é mais próximo de:
a. 22.
b. 50.
c. 100.
d. 200.
e. 400.
Veja o vídeo de resolução:
Questão 14
(Enem 2016) Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 – x2, sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a 2/3 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel.
Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
a. 18
b. 20
c. 36
d. 45
e. 54
Veja o vídeo de resolução:
Encontrou algum erro no gabarito nas questões de Funções no Enem nesta página? Deixe nos comentários abaixo para que possamos corrigir!
Siga-nos no instagram: @ofoconoenem e acompanhe novidades sobre o Enem em tempo real.




Comente