15 Questões de Probabilidade no Enem

A Probabilidade é o campo da matemática que estuda a probabilidade de um evento aleatório ocorrer. Para conseguir resolver as questões sobre o assunto é necessário que aluno tenha em mente alguns conceitos básicos, tais como: espaço amostral, evento e experimento aleatório.

Além disso, o estudante precisa conhecer a fórmula básica da probabilidade, uma vez que com ela será possível resolver a maioria dos exercícios da prova. Veja abaixo:

Por ser um tema constantemente presente no nosso dia a dia, a Probabilidade é dos assuntos mais abordados na prova de matemática no Enem. As questões de probabilidade no Enem sempre relacionam-se com fatos do nosso cotidiano e exigem bastante a atenção do aluno em relação a interpretação do enunciado.

As questões de Probabilidade abaixo são dos últimos Enem. Logo após cada questão, basta clicar “Ver resposta” para visualizar o gabarito da questão e um vídeo com a resolução detalhada do exercício para você revisar o conteúdo. Confira!

Resolvas as questões de Probabilidade no Enem

Questão 01

(Enem 2015) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso.

Qual a probabilidade de a senha sorteada ser um número de 1 a 20?

a. 1/100
b. 19/100
c. 20/100
d. 21/100
e. 80/100

Questão 02

(Enem 2010 2ª aplicação) Em uma reserva florestal existem 263 espécies de peixes, 122 espécies de mamíferos, 93 espécies de répteis, 1 132 espécies de borboletas e 656 espécies de
aves.

Se uma espécie animal for capturada ao acaso, qual a probabilidade de ser uma borboleta?

a. 63,31%
b. 60,18%
c. 56,52%
d. 49,96%
e. 43,27%

Questão 03

(Enem 2017 – 2ª aplicação) Um programa de televisão criou um perfil em uma rede social, e a ideia era de que esse perfil fosse sorteado para um dos seguidores, quando esses fossem em número de um milhão. Agora que essa quantidade de seguidores foi atingida, os organizadores perceberam que apenas 80% deles são realmente fãs do programa. Por conta disso, resolveram que todos os seguidores farão um teste, com perguntas objetivas referentes ao programa, e só poderão participar do sorteio aqueles que forem aprovados. Estatísticas revelam que, num teste dessa natureza, a taxa de aprovação é de 90% dos fãs e de 15% dos que não são fãs.

De acordo com essas informações, a razão entre a probabilidade de que um fã seja sorteado e a probabilidade de que o sorteado seja alguém que não é fã do programa é igual a

a. 1
b. 4
c. 6
d. 24
e. 96

Questão 4

(Enem 2017) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade da ocorrência de chuva nessa região.

Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?

Questão 05

(Enem 2013) Numa escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas lı́nguas estrangeiras, inglês e espanhol. Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.

Escolhendo-se um aluno dessa escola ao acaso e sabendo-se que ele não fala inglês, qual a probabilidade de que esse aluno fale espanhol?

Questão 06

(Enem 2017) Uma aluna estuda numa turma de 40 alunos. Em um dia, essa turma foi dividida em três salas, A, B e C, de acordo com a capacidade das salas. Na sala A ficaram 10 alunos, na B, outros 12 alunos e na C, 18 alunos. Será feito um sorteio no qual, primeiro, será sorteada uma sala e, posteriormente, será sorteado um aluno dessa sala.

Qual é a probabilidade de aquela aluna específica ser sorteada, sabendo que ela está na sala C?

a. 1/3
b. 1/18
c. 1/40
d. 1/54
e. 7/18

Questão 07

(Enem 2011) Em um jogo disputado em uma mesa de sinuca, há 16 bolas: 1 branca e 15 coloridas, as quais, de acordo com a coloração, valem de 1 a 15 pontos (um valor para cada bola colorida). O jogador acerta o taco na bola branca de forma que esta acerte as outras, com o objetivo de acertar duas das quinze bolas em quaisquer caçapas. Os valores dessas duas bolas são somados e devem resultar em um valor escolhido pelo jogador antes do início da jogada. Arthur, Bernardo e Caio escolhem os números 12, 17 e 22 como sendo resultados de suas respectivas somas.

Com essa escolha, quem tem a maior probabilidade de ganhar o jogo é

Questão 08

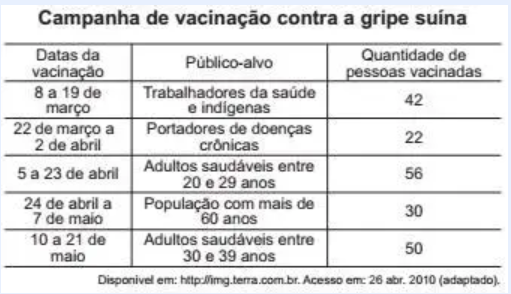
(Enem 2011) Todo o país passa pela primeira fase de campanha de vacinação contra a gripe suína (H1N1). Segundo um médico infectologista do Instituto Emilio Ribas, de São Paulo, a imunização “deve mudar”, no país, a história da epidemia. Com a vacina, de acordo com ele, o Brasil tem a chance de barrar uma tendência do crescimento da doença, que já matou 17 mil no mundo. A tabela apresenta dados específicos de um único posto de vacinação.

Escolhendo-se aleatoriamente uma pessoa atendida nesse posto de vacinação, a probabilidade de ela ser portadora de doença crônica é

Questão 09

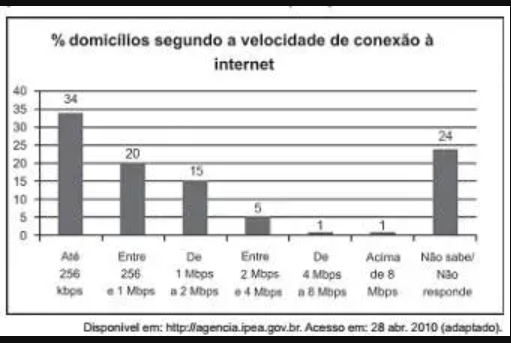
(Enem 2011) O gráfico mostra a velocidade de conexão à internet utilizada em domicílios no Brasil. Esses dados são resultado da mais recente pesquisa, de 2009, realizada pelo Comitê Gestor da Internet (CGI).

Escolhendo-se, aleatoriamente, um domicı́lio pesquisado, qual a chance de haver banda larga de conexão de pelo menos 1Mbps neste domicı́lio?

Questão 10

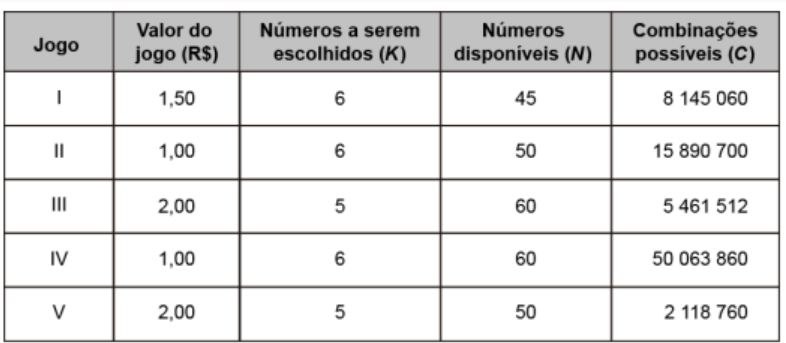
(Enem Digital 2020) Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.

Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.

Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o

Questão 11

(Enem Digital 2020) Um apostador deve escolher uma entre cinco moedas ao acaso e lançá-la sobre uma mesa, tentando acertar qual resultado (cara ou coroa) sairá na face superior da moeda.

Suponha que as cinco moedas que ele pode escolher sejam diferentes:

Nesse jogo, qual é a probabilidade de o apostador obter uma face “cara” no lado superior da moeda lançada por ele?

Questão 12

(Enem 2019) O dono de um restaurante situado às margens de uma rodovia percebeu que, ao colocar uma placa de propaganda de seu restaurante ao longo da rodovia, as vendas aumentaram. Pesquisou junto aos seus clientes e concluiu que a probabilidade de um motorista perceber uma placa de anúncio é 1/2. Com isso, após autorização do órgão competente, decidiu instalar novas placas com anúncios de seu restaurante ao longo dessa rodovia, de maneira que a probabilidade de um motorista perceber pelo menos uma das placas instaladas fosse superior a 99/100.

A quantidade mínima de novas placas de propaganda a serem instaladas é

Questão 13

(Enem 2021) O organizador de uma competição de lançamento de dardos pretende tornar o campeonato mais competitivo. Pelas regras atuais da competição, numa rodada, o jogador lança 3 dardos e pontua caso acerte pelo menos um deles no alvo. O organizador considera que, em média, os jogadores têm, em cada lançamento, 1/2 de probabilidade de acertar um dardo no alvo.

A fim de tornar o jogo mais atrativo, planeja modificar as regras de modo que a probabilidade de um jogador pontuar em uma rodada seja igual ou superior a 9/10. Para isso, decide aumentar a quantidade de dardos a serem lançados em cada rodada.

Com base nos valores considerados pelo organizados da competição, a quantidade mínima de dardos que devem ser disponibilizados em uma rodada para tornar o jogo mais atrativo é

Questão 14

(Enem 2018) Para ganhar um prêmio, uma pessoa deverá retirar, sucessivamente e sem reposição, duas bolas pretas de uma mesma urna.

Inicialmente, as quantidades e cores das bolas são como descritas a seguir;

• Urna A – Possui três bolas brancas, duas bolas pretas e uma bola verde;
• Urna B – Possui seis bolas brancas, três bolas pretas e uma bola verde;
• Urna C – Possui duas bolas pretas e duas verdes;
• Urna D – Possui três bolas brancas e três bolas pretas;

A pessoa deve escolher uma entre as cincos opções apresentadas:

• Opção 1 – Retirar, aleatoriamente, duas bolas da urna A;
• Opção 2 – Retirar, aleatoriamente, duas bolas da urna B;
• Opção 3 – Passar, aleatoriamente, uma bola da urna C para a urna A; após isso , retirar, aleatoriamente, duas bolas da urna A 
• Opção 4 – Passar, aleatoriamente, uma bola da urna D para a urna C; após isso, retirar, aleatoriamente, duas bolas da urna C;
• Opção 5 – Passar, aleatoriamente, uma bola da urna C para a urna D; após isso, retirar, aleatoriamente, duas bolas da urna D.

Com o objetivo de obter a maior probabilidade possível de ganhar o prêmio, a pessoa deve escolher a opção

Questão 15

(Enem 2020) Amigo secreto é uma brincadeira tradicional nas festas de fim de ano. Um grupo de amigos se reúne e cada um deles sorteia o nome da pessoa que irá presentear. No dia da troca de presentes, uma primeira pessoa presenteia seu amigo secreto. Em seguida, o presenteado revela seu amigo secreto e o presenteia. A brincadeira continua até que todos sejam presenteados, mesmo no caso em que o ciclo se fecha. Dez funcionários de uma empresa, entre eles um casal, participarão de um amigo secreto. A primeira pessoa a revelar será definida por sorteio.

Qual é a probabilidade de que a primeira pessoa a revelar o seu amigo secreto e a última presenteada sejam as duas pessoas do casal?

a. 1/15

b. 1/45

c. 1/50

d. 1/90

e. 1/100

Você também pode gostar:

• 50 questões de Matemática Financeira no Enem
• Matemática Básica no Enem: O que estudar
• 5 tópicos Matemática que mais caem no Enem

Encontrou algum erro no gabarito nas questões de Probabilidade no Enem nesta página? Deixe nos comentários abaixo para que possamos corrigir!